Cuando una máquina aprende
Ivan Moreno, 15 December 2018
Estudiamos conceptos de la teoría estadística del aprendizaje en la última parte de la materia. Hicimos unos ejercicios para ilustrarlos.
Cuando queremos clasificar información a partir de una muestra de esta, generalmente usamos aprendizaje supervisado, porque es popular. Pero hay detalles que hay que tomar en cuenta para crear un clasificador decente. Estos detalles son estudiados en la teoría estadística del aprendizaje (el nombre puede variar un poco).
Suposiciones
Todo empieza cuando tenemos un conjunto de datos $X$ (una muestra) y un conjunto de etiquetas $Y$ que nos dicen a qué clase pertenecen, y hacemos unas suposiciones sencillas:
- Existe $ f : X \rightarrow Y $ que desconocemos
- $ y^i = f(x^i) + e $ donde $e$ es un error aleatorio
La tarea es encontrar una hipótesis que se acerque lo suficiente a esa función desconocida. O mejor aún, encontrar la mejor hipótesis posible. Para poder medir el rendimiento ocupamos definir una función de pérdida $loss(h, x)$.
A partir de esta pérdida, tenemos dos tipos de errores: error dentro de muestra ($E_{in}$) y error fuera de muestra ($E_{out}$). Para decir que una máquina aprende, ocupamos que $E_{in} \approx 0$ y que $E_{out} \approx E_{in}$. Es decir, la computadora aprende a particularizar dentro del conjunto de entrenamiento y al mismo tiempo aprende a generalizar para datos que nunca ha visto.
Quizá suene fácil si simplemente conseguimos datos, los limpiamos y los metemos en un algoritmo clásico de aprendizaje supervisado. Pero hay una cosa llamada dimensión vc que nos indica el máximo número de datos que podemos separar perfectamente con nuestra hipótesis. Nos da una medida de la complejidad de nuestro modelo, y si lo complicamos demasiado y tenemos pocos datos, el algoritmo no aprenderá. Lo mejor de esta dimensión es que si transformamos mucho nuestros datos manualmente, incrementa, aunque no nos demos cuenta. Para ver el comportamiento de la dimensión vc están las siguientes gráficas de una función que depende del tamaño del conjunto de entrenamiento.
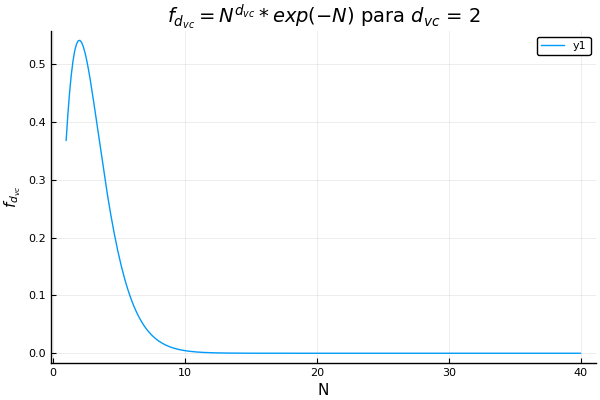
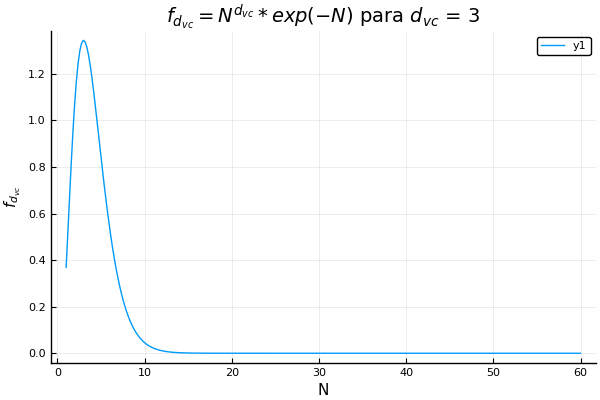
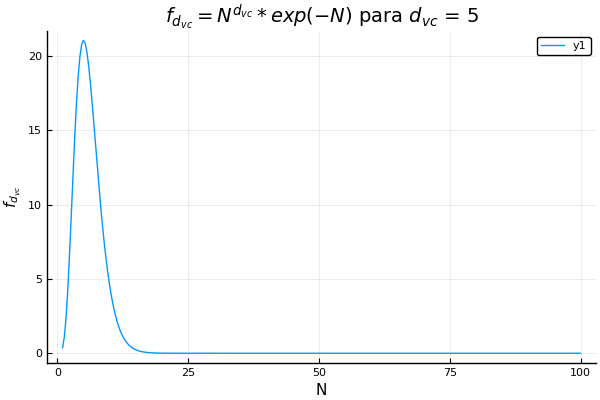
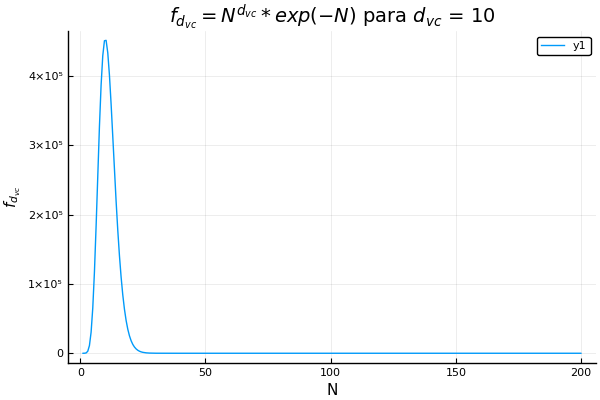
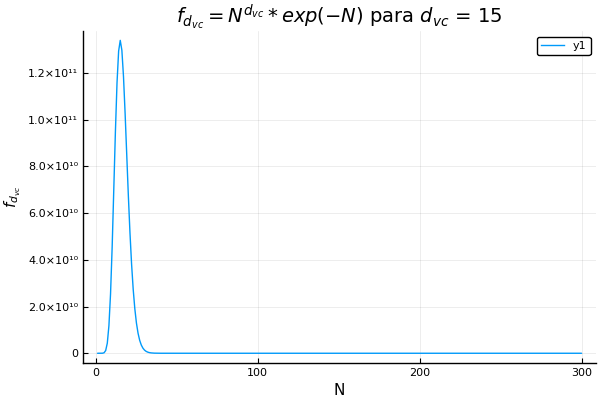
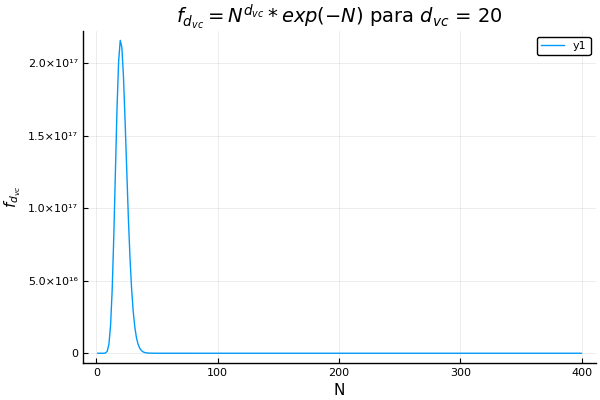
Sesgo-Varianza
Probablemente has pensado que no podemos tener particularización y generalización perfectas al mismo tiempo, y es cierto, tenemos que buscar un balance entre ambas. Además, cuando estamos probando hipótesis distintas, tenemos que encontrar un balance entre el sesgo y la varianza.
El sesgo es la desviación que tiene una hipótesis de la función desconocida, o del valor real que debería tener. La varianza es la medida de que tan distintas son las hipótesis que tenemos.
Veamos un ejemplo: queremos aproximar $sen(\pi x)$ con funciones constantes y lineales. En las siguientes imágenes podemos ver los resultados.
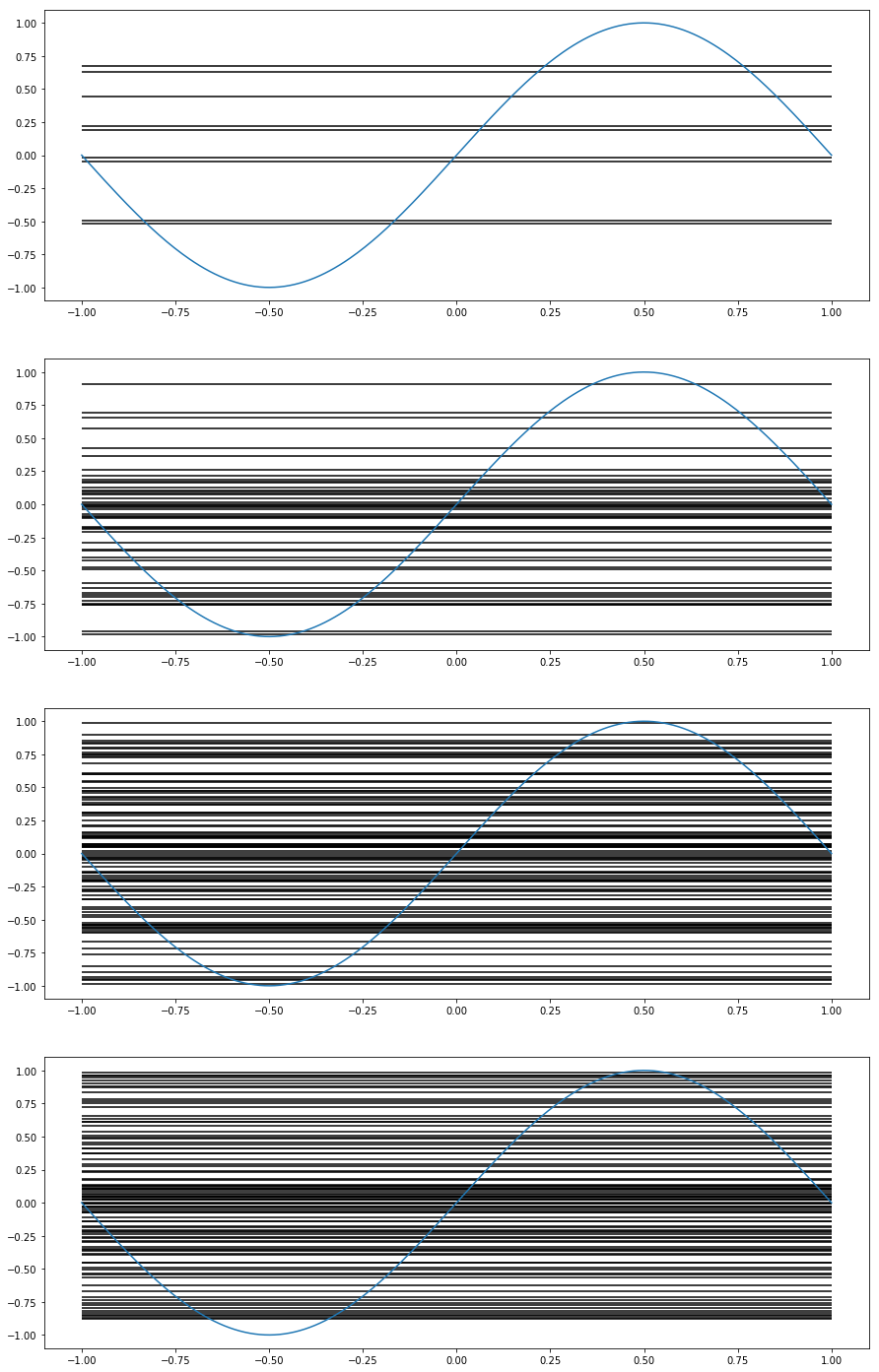
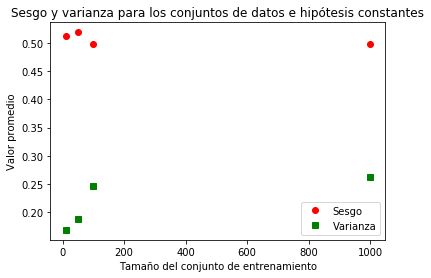
Para aproximaciones constantes tenemos poca varianza entre las hipótesis pero el sesgo es alto, porque obviamente hay mucha diferencia entre una función constante y una senoidal.
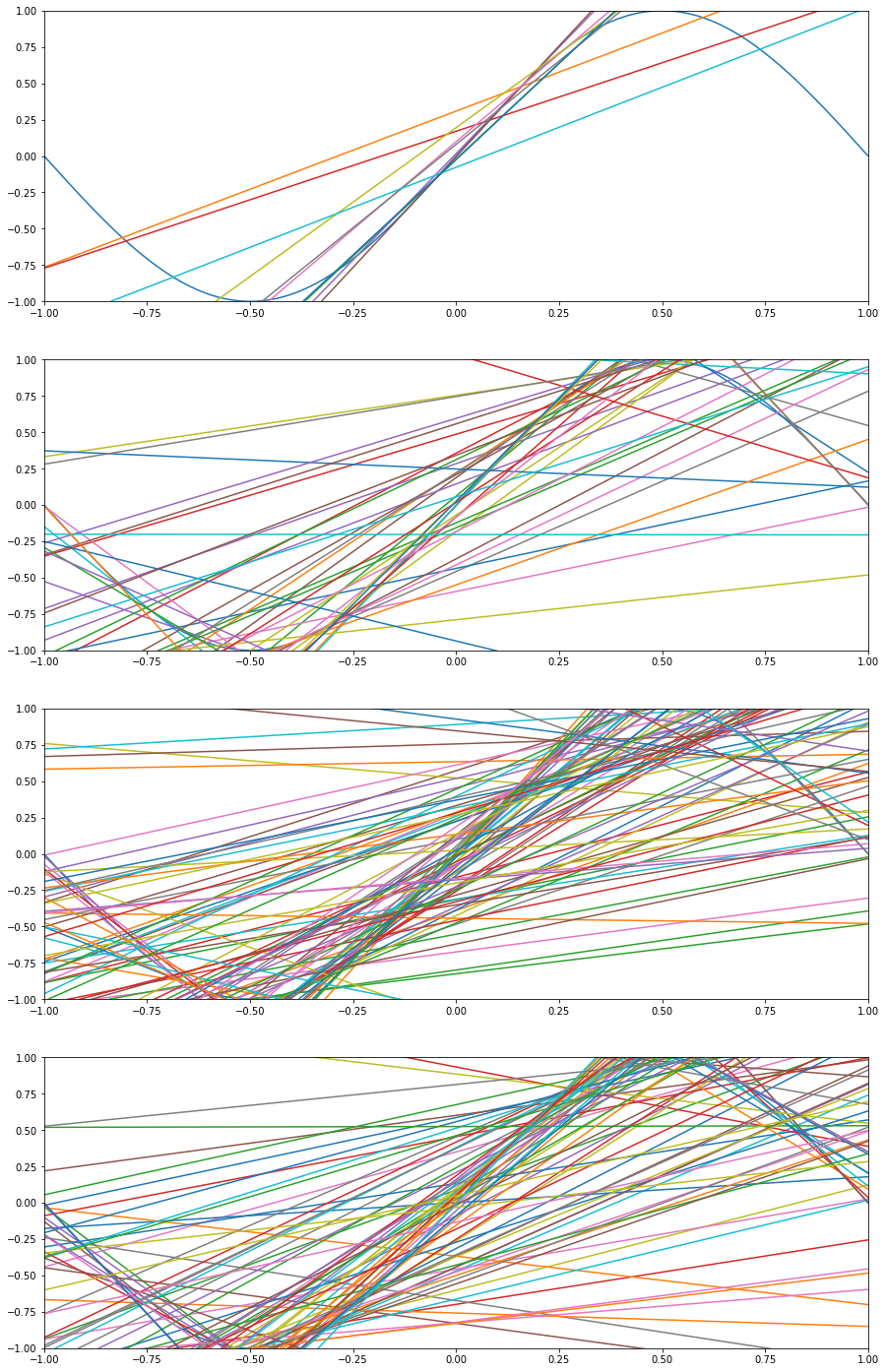
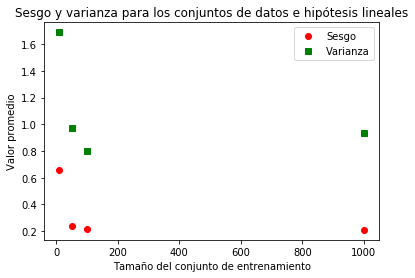
Para aproximaciones lineales tenemos un sesgo mucho menor que en el caso anterior, pero por las distintas pendientes que tienen, la varianza es alta.
Ruido en la muestra
Cuando conseguimos una muestra de los datos que queremos clasificar, posiblemente tendrá ruido. Este ruido puede ser determinista (lo que es mejor) o puede ser estocástico.
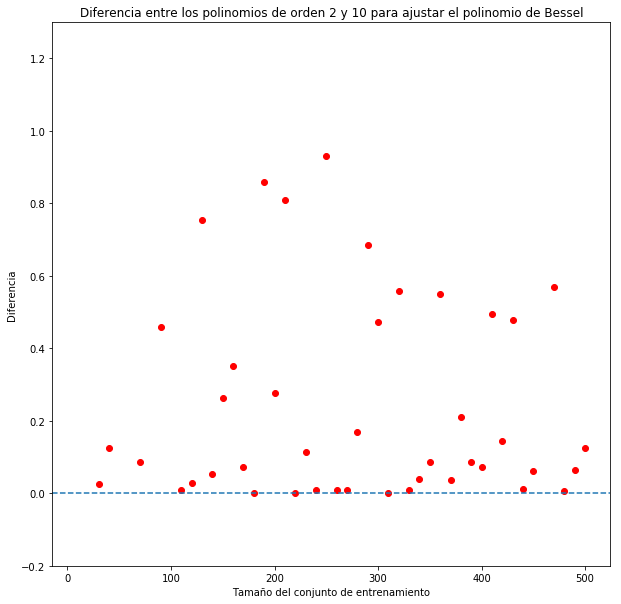
En la siguiente imagen se compara el ajuste generado por un polinomio de orden 2 contra uno de orden 10 para aproximar un polinomio de Bessel de orden 3 con ruido estocástico. Para compararlos, calculé el error en muestra de ambos de modelos y resté el error del polinomio de orden 2 del error del polinomio de orden 10: $ Diferencia = E_{in_{10}} - E_{in_2} $.
Al menos en este ejemplo un modelo más sencillo aproximó mejor en una situación con ruido estocástico.